[深度學習練習] [Deep Learning Practice] 神經網路入門（五）- 卷積神經網路 X 實作

上一集中，紀錄卷積神經網路的基本理解，

這一集就會使用卷積神經網路來預測 mnist 的 data，

做圖像辨識的練習。

------------------------------------------------------------------------------------------------------------

一、卷積神經網路實作

和基礎神經網路實作一樣，我們先用 mnist 提供的數字圖片，

來讓卷積神經網路學習，藉此讓自己更瞭解卷積神經網路該怎麼寫。



上一篇中，我們知道卷積神經網路，最重要的東西就是這個卷積，也就是 filter，

除此之外，他與基礎神經網路沒有什麼差別，

所以寫法邏輯非常像，先定義卷積神經網路的長相，再定義最佳化神經網路的方法。

但是，在定義卷積神經網路模型之前，我們先把 filter 寫出來，還有 maxpooling。

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

mnist = input_data.read_data_sets('/tmp/data', one_hot = True)

n_classes = 10
batch_size = 128

# height * width
x = tf.placeholder('float',[None, 784])
y = tf.placeholder('float')

def conv2d(x, W, b, strides=1):
    x = tf.nn.conv2d(x, W, strides=[1, strides, strides, 1], padding='SAME')
    x = tf.nn.bias_add(x, b)
    return tf.nn.relu(x)

def maxpool2d(x, k=2):
    return tf.nn.max_pool(x, ksize=[1, k, k, 1], strides=[1, k, k, 1], padding='SAME')


除了 conv2d 以及 maxpool2d 以外，幾乎都和基礎神經網路一樣的開頭。

這個 conv2d 是 TF 為我們準備好的定義 filter 方法，非常的方便，

變數 x 是輸入，W 是定義 filter size 的變數，b 是計算 y = Ax + b 的那個截距，

至於 stride，就是往各個方向卷積時，每一次要跨的步數。

maxpool2d 是上一集中留下的伏筆，上集提到除了卷積外，

我們還會用 maxpooling 來加速運算以及避免 overfitting，不是一定要，但加了會更好就加。

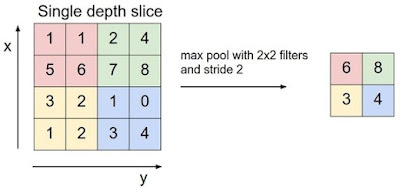
那 maxpooling 是什麼概念呢？

把像素變模糊，絕對沒有特殊處理，單純變模糊而已，

2*2變成1*1這樣子，變得方法可能就隨便取個最大值，也可以自己定義。

如果還是不懂意思，把眼睛瞇起來，這樣就是 maxpooling ，簡單吧？

------------------------------------------------------------------------------------------------------------

二、定義卷積神經網路

好，現在可以開始定義卷積神經網路，沒有太大特色，跟之前很像，

在剛剛的程式碼中，加入以下，

def convolutional_neural_network(x):

    # 一樣定義每一層的神經層的 weight 與 bias，conv1 and conv2 下方細講。
    weights = {'W_conv1':tf.Variable(tf.random_normal([5,5,1,32])), 
                'W_conv2':tf.Variable(tf.random_normal([5,5,32,64])), 
                'W_fc':tf.Variable(tf.random_normal([7*7*64, 1024])), 
                'out':tf.Variable(tf.random_normal([1024, n_classes]))}
    biases = {'b_conv1':tf.Variable(tf.random_normal([32])), 
                'b_conv2':tf.Variable(tf.random_normal([64])), 
                'b_fc':tf.Variable(tf.random_normal([1024])), 
                'out':tf.Variable(tf.random_normal([n_classes]))}

    # 把原本被我們改成 784 的向量轉回 28 * 28，reshape很重要，下一集細講。
    x = tf.reshape(x, shape=[-1,28,28,1])

    # 以下定義層層之間的安排
    conv1 = tf.nn.relu(conv2d(x, weights['W_conv1'], biases['b_conv1']))
    conv1 = maxpool2d(conv1)

    conv2 = tf.nn.relu(conv2d(conv1, weights['W_conv2'], biases['b_conv2']))
    conv2 = maxpool2d(conv2) fc = tf.reshape(conv2, [-1, 7*7*64]) fc = 

    tf.nn.relu(tf.matmul(fc, weights['W_fc']) + biases['b_fc'])
    output = tf.matmul(fc, weights['out']) + biases['out']

    return output

好，講個卷積之中很重要的東西，如果不懂的話，就無法自己寫卷積神經網路。

上一集中只有稍微提到 filter 的概念，現在要仔細講講 filter size 要如何定義和如何對應。

我們用一篇在 2010 年圖片分類大賽拿過冠軍的模型來講解一下，

ImageNet Classification with Deep Convolutional Neural Networks

該文中的 figure 2 即是此團隊使用的卷積神經網路模型，

看起來好像很難，跟著解釋，看過一次，這個跨入卷積世界的第一關卡就可以輕易克服惹。

首先辨認一下，什麼是局部感知 (partial connection)，什麼是全域感知 (full connection)。

全域感知如像第 7 層到第 8 層一樣，

第 8 層中的每一個元素都有來自第 7 層中的每一個元素的輸入，

像基礎神經網路的運算一樣。(這篇的第一張圖)

而局部感知就不一樣了，如第 2 層中的某單一元素可能只由第 1 層中的某幾個元素組合，

類似像這樣的圖解概念。

Full : R1 元素由 G1&G2&G3&G4&G5 組合，R2 元素也由 G1&G2&G3&G4&G5 組合

Partial : R1 元素只由 G1&G2&G3 組合，R2 元素只由 G2&G3&G4 組合

理解完局部感知 (partial connection) 和全域感知 (full connection) 後，看回結構。

第一層到第二層之間，發生了什麼事情呢？

第一層 : 224 * 224 * 3 (上一集中有說到圖片會有長寬高，你也可以看成三維矩陣)

第二層 : 55 * 55 * 48 * 2 ( 2 是上下層，一共兩個 GPU )

為什麼會縮成這樣子呢？

其實第一層到第二層之間，經過了 48 * 2 個 11 * 11 的 filters，每個 filter 每次會跨 4 步，

所以 224 / 4 ~ 55，你可能想說明明是 56 不要唬，

因為我們一開始就使用了 11 格，還有最後面邊界也要留 11 格，

你可能想說，這樣也不是 55，

這其實是卷積的另外一個重點，邊界定義的問題，因為太複雜，

我們只是亂學，就記得 224 / 4 = 55 這樣就可以惹。

那從 3 變成 48 又是什麼意思呢？

意思是，我們有 48 種同樣大小但不同的卷積核 ( filter )，所以可以取出 48 種特徵！

再來，第二層到第三層之間，發生了什麼事情呢？

比之一和二層，這一次我們多了一個以 2 * 2 為單位的  maxpooling，

然後這一次我們的 filter stride 是 1，所以 55 / 1 = 55，但因為有 maxpooling，

55 / 2 ~27，而得到了下一層的 27 * 27 * 128，接下來以此類推。

為什麼了解這個是重要的呢？

因為這樣我們才看得懂，這段在寫什麼。

    weights = {'W_conv1':tf.Variable(tf.random_normal([5,5,1,32])), 
                'W_conv2':tf.Variable(tf.random_normal([5,5,32,64])), 
                'W_fc':tf.Variable(tf.random_normal([7*7*64, 1024])), 
                'out':tf.Variable(tf.random_normal([1024, n_classes]))}

conv1 : 以 32 個 5 * 5 filters，以每次跨一步對 28 * 28 * 1 做卷積

conv2 : 以 64 個 5 * 5 filters，以每次跨一步對 14 * 14 * 32 做卷積

W_fc : 這是 full connection，直接以矩陣轉換，沒有 filter

中間因為經過了兩次的 maxpool 所以長寬從 28 -> 14 -> 7。

好，到這邊，希望大家有看懂我們卷積神經網路的架構，

接下來是最佳化。

------------------------------------------------------------------------------------------------------------

三、最佳化卷積神經網路

在神經網路最佳化上面，並沒有什麼特別的，我就直接附上程式碼。

def train_neural_network(x):
    prediction = convolutional_neural_network(x)
    cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(prediction,y))

    optimizer = tf.train.AdamOptimizer().minimize(cost)

    hm_epochs = 3

    with tf.Session() as sess:
        sess.run(tf.initialize_all_variables())

        for epoch in range(hm_epochs):
            epoch_loss = 0
            for _ in range(int(mnist.train.num_examples/batch_size)):
                epoch_x, epoch_y = mnist.train.next_batch(batch_size)
                _, c = sess.run([optimizer,cost], feed_dict = {x: epoch_x, y: epoch_y})
                epoch_loss += c
            print ('Step', epoch, 'out of', hm_epochs, 'loss:', epoch_loss)

        correct = tf.equal(tf.argmax(prediction,1), tf.argmax(y,1))

        accuracy = tf.reduce_mean(tf.cast(correct, 'float'))
        print ("Optimization Finished!")
        print ('Accuracy:' ,accuracy.eval({x:mnist.test.images, y:mnist.test.labels}))

train_neural_network(x)


完成後，執行此段程式碼，等個十分鐘，應該會看到這個。

好，雖然沒有達到超高的準確率，

但還是比基礎神經網路還要高，而且我們只訓練了 3 回合。

希望藉由這個，可以讓大家感受到 Convolutional Neural Network 的實力，

這邊附上官方程式碼。 Link

接下來，我們將會運用 CNN 的圖片辨識能力，來幫我們預測台股指數！

------------------------------------------------------------------------------------------------------------

Reference

[1] Practical Machine Learning Problem

[2] 圖解機器學習

[3] Coursera - Machine Leanring 

[4] A tour of machine learning algorithms

[5] Deep Learning Book

[6] Threshold Potential

[7] Activation Function

[8] Receptive fields and functional architecture of monkey striate cortex

下一集：

[深度學習練習] [Deep Learning Practice] 神經網路入門（六）- 卷積神經網路 X 台指